دوال الاكسل المالية للاستثمار والاقتراض

عزيزي القارئ يعتبر مجال العلوم المالية من المجالات العلمية التطبيقية التي تعتمد على تحليل كم هائل من البيانات وإجراء العمليات الحسابية البسيطة والمعقدة والتي تتصف بشيء من التكرارية وتأخذ وقتاً كبيراً وجهداً من العاملين في هذا المجال، فان برنامج الاكسل Excel يعتبر من أفضل البرمجيات التي تلبي متطلبات العاملين في هذا المجال فيما إذا تمكنوا من تعلم آلية التعامل معه وأسلوب إدخال البيانات ومعالجتها وتحليلها واستخلاص المعلومات اللازمة لاتخاذ القرارات المالية.

يتضمن مايكروسوفت اكسل أكثر من 55 دالة مالية جاهزة، والتي تساعد الإداري في معالجة بياناته واتخاذ القرارات بالسرعة والدقة اللازمة، وتأتى أهمية هذه الدوال في أنها تخفف على المستخدم عبئ حفظ وتذكر كيفية استخدام وحساب العلاقات المالية وخاصة العلاقات التي تحتاج إلى حسابات طويلة ومعقدة، إذ يطلب الحاسوب من المستخدم عند إدراج دالة مالية معينة تحديد أماكن البيانات اللازمة لتطبيق الدالة (الخلايا التي تضم البيانات التي سنعالجها) من خلال صناديق الحوار التي تظهر على شاشة الحاسوب.

لمزيد من المعلومات عن الأكسل:

عزيزي القارئ سنشرح في مقالات أخرى بعض هذه الدوال المتعلقة بالاستثمار والقروض وهي: RATE، PMT، PV, FV، NPER وهذه الدوال موجودة ضمن فئة الدوال “مالية Financial”

للتعلم آلية التعامل مع دوال الإكسل

اما في هذا المقال فسنستعرض بعض المفاهيم والمصطلحات الضرورية التي يجب عليك عزيزي القارئ التعرف عليها ان كنت من غير المختصين في مجال العلوم المالية والمصرفية، اما المختصين فيمكنهم تخطي هذا المقال الى المقالات التي تشرح الدوال الآتية:

الدالة RATE لحساب معدل الفائدة بالفترة الزمنية لقرض أو استثمار
الدالة PMT لحساب قيمة القسط اللازم دفعه لتسديد قرض
الدالة FV لحساب القيمة المستقبلية
الدالة NPER لحساب عدد الدفعات
الدالة PV لحساب القيمة الحالية

مفاهيم ومصطلحات

سنذكر فيما يلي ببعض المفاهيم والمصطلحات المالية الضرورية قبل التطرق للدوال المالية[1]:

الفائدة Interest: من وجهة نظر المستثمر (صاحب رأس المال) هي العائد أو المردود المادي الناتج عن استثمار مبلغ من المال خلال فترة زمنية محددة بمعدل فائدة سنوي محدد، وتدعى فائدة الاستثمار. أما من وجهة نظر المقتَرِض هي ثمن الأموال المقتَرَضة خلال فترة زمنية محددة بمعدل فائدة سنوي محدد، وتدعى فائدة القرض.

المبلغ المستثمر Investment Amount: هو عبارة عن المبلغ المودع أو المبلغ المقترض والذي يترتب على استخدامه تعويض مادي (الفائدة) يلتزم الشخص المدين (المقتَرِض) تجاه الدائن صاحب رأس المال (المقرِض).

معدل الفائدة Rate of Interest: هو العائد الناتج عن استثمار وحدة رأس المال في نهاية دورة زمنية، وقد جرت العادة على استخدام الدورة الزمنية فترة السنة، وكذلك استخدام مائة وحدة من النقود عند تحديد معدل الفائدة، مثال: معدل الفائدة خمسة بالمائة وتكتب 5% أو 0.05.

الدورة الزمنية The Period (Time): هي المدة التي يستحق بعدها صرف مبلغ الفائدة. فإذا كان الاتفاق بين الدائن والمدين على سداد قيمة فائدة رأس المال المستثمر في نهاية:

كل سنة فإن الدورة الزمنية هي السنة. ويكون معدل الفائدة المستخدم سنوي.
كل شهر فإن الدورة الزمنية هي الشهر. ويكون معدل الفائدة المستخدم شهري.
كل ثلاثة أشهر فإن الدورة الزمنية هي ربع سنة. ويكون معدل الفائدة المستخدم ربع سنوي.
كل ستة أشهر فإن الدورة الزمنية هي نصف سنة. ويكون معدل الفائدة المستخدم نصف سنوي.

الفائدة البسيطة Simple Interest: هي الفائدة المترتبة على أصل المبلغ المستثمر عن وحدة زمنية محددة (سنة مثلاً) يتم الاتفاق عليها بمعدل فائدة معلوم لدورة زمنية محددة، حيث يسدد مقدار الفائدة في نهاية الوحدة الزمنية ويبقى رأس المال الأصلي ثابتاً.

الفائدة المركبة Compound Interest: هي الفائدة المترتبة على المبلغ المستثمر التي تضاف إليه في نهاية كل وحدة زمنية (سنة عادة) لتستثمر من جديد وتنتج فائدة جديدة، أي أن الفائدة المركبة تتحول في نهاية كل وحدة زمنية إلى رأس مال جديد تكون قابلة للاستثمار.

القيمة الحالية Present Value: هي قيمة مبلغ الاستثمار أو القرض الآن، أي بداية فترة الاستثمار، ويرمز له بـ Pv.

القيمة المستقبلية Future Value: هي جملة مبلغ الاستثمار الحالي أو القرض الحالي بعد n سنة، أي نهاية فترة الاستثمار، ويرمز له بـ Fv.

العلاقة بين القيمة الحالية لمبلغ وقيمته المستقبلية[2]:

Fv= Pv(1+Rate)ⁿ

حيث:

Fv: القيمة المستقبلية (جملة المبلغ) لمبلغ حالي بعد n سنة.

Pv: المبلغ الحالي (رأس المال) أو المبلغ الأصلي.

Rate: معدل الفائدة السنوي.

n: مدة الاستثمار (مدة الاقتراض) وتقاس دائماً بالسنوات.

الدفعات الدورية Periodic Payments: هي دفعات متساوية منتظمة تدفع بقيم متساوية وعلى فترات زمنية متساوية، قد تكون سنوية، أو نصف سنوية، أو ربع سنوية، أو كل شهرية ..، وهذه الدفعات تأخذ قيم معينة في كل لحظة من لحظات الزمن، ولكن أهم اللحظات هما اللحظتين الآتيتين:

اللحظة الحالية: (الآن) وتسمى فيها قيمة الدفعات المتساوية بالقيمة الحالية لهذه الدفعات.
اللحظة الأخيرة: أي لحظة نهاية الفترة التي تسدد من أجلها الدفعة الأخيرة وتسمى قيمة الدفعات فيها بالقيمة المستقبلية لهذه الدفعات، أو جملة الدفعات.

أنواع الدفعات من حيث لحظة التسديد، وتقسم إلى نوعين:

الدفعات العادية Regular Payments: وهي التي تدفع في نهاية الدورة الزمنية (مثلاً السنة)، وتسمى أيضاَ بدفعات السداد، وسميت بهذا الاسم لأنه إذا حصل شخص على قرض الآن على أن يرده على أقساط فلن يكون الأمر منطقي أن يقوم بتسديد أول دفعة من أقساطه الآن، لأن هذا يعني أن المقترض لن يحصل على كامل مبلغ القرض.
الدفعات الفورية Instant Payments: وهي التي تدفع في بداية الدورة الزمنية (مثلاً السنة) وتسمى أيضاَ بدفعات الاستثمار وسميت بهذا الاسم لأنه إذا أراد شخص أن يستثمر المال في مصرف مثلاً على شكل دفعات مالية متساوية فلا يبدأ حساب الأرباح (الفوائد) إلا من تاريخ مباشرة الدفعة الأولى.

محدّدات عملية الاقتراض Determinates of borrowing process:

عندما يقترض أحد الأشخاص مبلغاً ما من أحد المصارف فإنّه عادةً يتفق على سداد القرض مع فوائده من خلال عدد من الأقساط المتساوية، وفي هذه الحالة فإنّ قيمة القرض التي يستطيع الشخص الحصول عليه تتحدّد وفقاً لقيمة القسط الذي يستطيع الشخص دفعه بشكل دوري (في نهاية أو بداية كل دورة) وعدد الأقساط التي يرغب المدين بدفعها، ومعدّل الفائدة الذي يفرضه المصرف (الدائن) على المدين، يحسب بإحدى المعادلتين الآتيتين[3]:

الدفعات عادية:

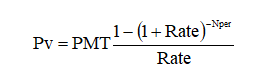
الدفعات فورية:

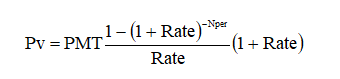
حيث:

Pv: قيمة القرض الذي يمكن للمدين استلامه الآن أو ما يعرف بالقيمة الحاليّة (Present Value).

PMT: قيمة القسط الدوري المتساوي الذي سيدفعه المدين للدائن لسداد القرض والفوائد وذلك في نهاية أو بداية كل دورة (Payment).

Rate: معدّل الفائدة (Interest Rate) الدوري الذي يطلبه الدائن من المدين والجدير بالذكر أنّ الدورة المتعلّقة بالمعدّل تتوافق مع الدورة المتعلّقة بالقسط فإذا كان القسط سنوياً فالمعدّل سنوي وإذا كان القسط شهرياً فالمعدّل شهري وهكذا..

Nper: عدد الدورات التي سيدفع المدين في نهاية أو بداية كل منها قسطاً، أي عدد الأقساط (Number Premium).

وبالتالي لمعرفة قيمة أياً من المحددات الأربع السابقة: (Pv أو PMT أو Rate أو Nper) يجب أن يكون معلوماً قيم باقي المحددات اعتماداً على إحدى العلاقتين السابقتين، أما باستخدام برنامج الكسل فإنه بمكننا استخدام الدوال الآتية والتي سنتناولها بالتفصيل في الفقرات اللاحقة: Pv، PMT، Rate، Nper.

محدّدات عملية الاستثمار Determinates of investment process:

عندما يريد أحد الأشخاص استثمار مبلغاً ما من أحد المصارف فإنّه عادةً يتفق على إيداع المبلغ على عدد من الدفعات المتساوية، وفي هذه الحالة فإنّ القيمة المستقبلية التي يستطيع الشخص الحصول عليه تتحدّد وفقاً لقيمة الدفعة الذي يستطيع الشخص دفعه بشكل دوري (في نهاية أو بداية كل دورة) وعدد الأقساط التي يرغب الشخص بدفعها، ومعدّل الفائدة المتفق عليه بين الشخص والمصرف، يحسب بإحدى المعادلتين الآتيتين[4]:

الدفعات عادية:

الدفعات فورية:

حيث:

Fv: القيمة المستقبلية لمبلغ أو لدفعات دوربة متساوية الذي يمكن للمستثمر استلامه في نهاية فترة الاستثمار أو ما يعرف بالقيمة المستقبلية (Future Value).

PMT: قيمة الدفعة الدورية المتساوية الذي سيدفعه المستثمر لسداد مبلغ الاستثمار وذلك في نهاية أو بداية كل دورة (Payment).

Rate: معدّل الفائدة (Interest Rate) الدوري المتفق عليه بين المستثمر والمصرف، والجدير بالذكر أنّ الدورة المتعلّقة بالمعدّل تتوافق مع الدورة المتعلّقة بالدفعة فإذا كانت الدفعة تدفع سنوياً فالمعدّل سنوي وإذا كان الدفعة تدفع شهرياً فالمعدّل شهري وهكذا..

Nper: عدد الدورات التي سيدفع المستثمر في نهاية أو بداية كل منها دفعة، أي عدد الدفعات (Number Premium).

وبالتالي لمعرفة قيمة أياً من المحددات الأربع السابقة: (Fv أو PMT أو Rate أو Nper) يجب أن يكون معلوماً قيم باقي المحددات اعتماداً على إحدى العلاقتين السابقتين، أما باستخدام برنامج الاكسل فإنه بمكننا استخدام الدوال الآتية والتي سنتناولها بالتفصيل في الفقرات اللاحقة: Fv، PMT، Rate، Nper.

تنويه: يستطيع برنامج الاكسل التمييز بين عمليّات الاستثمار والخصم (الاقتراض) المتعلّقة بمبلغ واحد وتلك المتعلّقة بعدد من المبالغ (الدفعات)، بحيث أنّه يطبّق المعادلات المبيّنة أعلاه حسب الحاجة.

ملاحظة هامة: قبل أن نشرح الدوال المالية المتعلقة بالاقتراض أو الاستثمار يجب تذكّر أمرين مهمين عند العمل على كل منها وهما:

1- التأكّد من الحفاظ على ثبات افتراضاتنا للفترات الزمنيّة الخاصّة بالمدفوعات والمدّة والمعدّل كأن نعمل وفق فترات (دفعات) شهريّة أو سنويّة.

2- من الأفضل أن نعتمد إشارة خاصّة للقيمة وذلك لبيان فيما إذا كان التدفق النقدي داخلاً أم خارجاً، ويجب أن نعطي الرصيد الأوّلي للقرض قيمة موجبة (بفرض أنّنا نحن المقترضون) لأنّه يمثّل تدفقاً نقدياً داخلاً، كما نعطي لأقساط أو دفعات القرض قيمة سالبة (بفرض أنّنا نحن أيضاً المقترضون) لأنّها تمثل تدفقاً نقدياً خارجاً، كما نلاحظ أنّ Excel يستخدم إشارات للقيم بالطريقة نفسها فهو يظهر التدفقات النقدية الداخلة بقيم موجبة والتدفقات النقدية الخارجية بقيم سالبة.

في النهاية أعزائي القراء أتمنى أن تكون هذه التدوينة مفيدة وتساعدكم لمعرفة المزيد عن الاكسل، وإلى لقاءات قادمة ومتجددة على مدونتكم مدونة النائب للعلوم والتكنلوجيا. وأريد أن أطلب منكم ألا تترددوا أبداً في طرح أي سؤال علينا في التعليقات أو من خلال صفحتنا الرسمية على الفيس بوك حيث نتواجد هناك باستمرار. وإذا كان لديكم استفسارات أخرى يمكنكم دائماً مرسلتنا عبر هذا الرابط.

وإلى لقاءٍ قريب.

[1] لمزيد من الايضاحات يمكن الرجوع إلى الكتب الرياضيات المالية

[2] كبية، محمد -2007- استخدام الحاسوب في العلوم المالية والمصرفية – مديرية الكتب والمطبوعات الجامعية – جامعة حلب- ص159

[3] دركزنلي، محمد سمير- 2016- الرياضيات المالية والتأمين – مديرية الكتب والمطبوعات الجامعية – جامعة حلب- ص119- 122.

[4] دركزنلي، محمد سمير (مرجع سابق) ص126-128

اقرأ أيضاً:

دوال الاكسل المالية للاستثمار والاقتراض

مفاهيم ومصطلحات

نُشر بواسطة Dr. Ibrahim Nayeb

أضف تعليق إلغاء الرد

مفاهيم ومصطلحات

شارك هذا الموضوع:

مرتبط

نُشر بواسطة Dr. Ibrahim Nayeb

أضف تعليق إلغاء الرد